(then repeat)
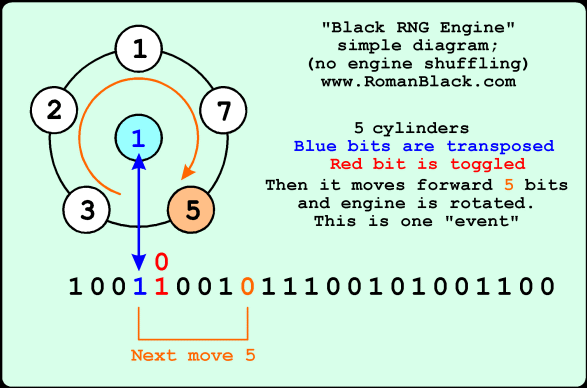
The diagram above shows an engine with 5 "cylinders" and one "held" bit. An engine event transposes the (blue) bits so the held bit is swapped with the bit in the cache. The engine event also toggles the next (red) bit. Then the engine moves forward 5 bits ready to repeat. The engine cylinders are rotated one place, so the next move distance will be 7 bits.
The engine will skip through the cache bits, processing some bits but not all. Over multiple passes there will be a very complex beat frequency of the cylinder values vs the length of the cache that scrambles the cache bits quite well but still in a complex pattern.
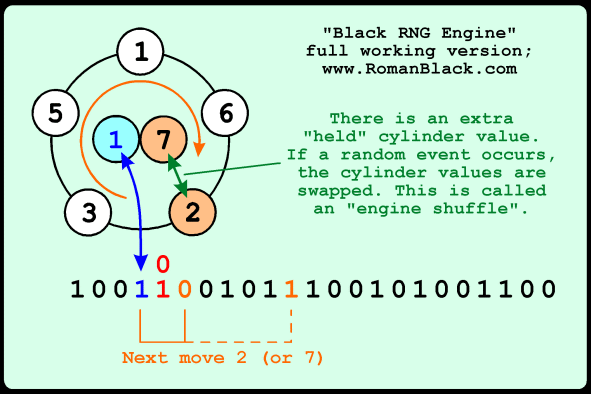
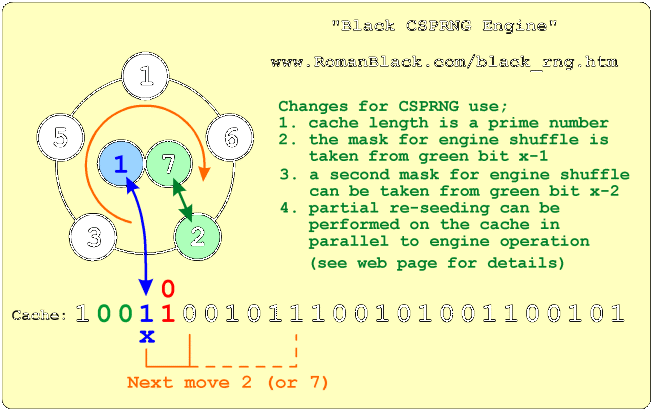
Above shows the same basic system, but with one addition. There is now a "held" cylinder value, as well as a held bit. When a random event is detected the cylinder values are swapped, this "engine shuffle" means that the engine has many possible configurations, and each engine configuration will scramble the cache bits with a different complex pattern.
If the engine is shuffled many times per pass through the cache then eventually any cache bit will have been processed by different configurations of the engine, at different times, and an unknown amount of times.
Also, as bits are picked up and put down in different locations bits will be transposed from areas of the cache that may not have been affected for many passes to areas that are being affected by passes now. Combined with the fact that the engine configuration changes over time this is scrambling new bits together with old bits that were previously scrambled by a vastly different engine configuration.
Originally I called this; "Transposing bits in both space AND time" and it is instrumental in generating the high level of chaos in this RNG.
The "random event" that causes the cylinder value swap can be anything of acceptable frequency including a real-world stimulus. For a self contained RNG I used a bitmask (typically 8 bits) compared to the last 8 bits that have been transposed. So on average, an engine shuffle will occur after every 256 engine events.
The Black RNG algorithm (actual implementation);
1. Transpose the held bit with current cache bit
1b. Shift a copy of the new held bit into the 8bit mask test
2. Toggle the bit after the current bit
3. Using X value from engine, move forward in cache, X bits
4. Rotate engine to next cylinder
5. Test the mask, see if it matches the last 8 transposed bits
5b. If it matches; swap the current cylinder value with held cylinder
(repeat)
Details of the implementation in C code
For convenience of indexing the bits in the cache, I just used 1 byte to represent each bit. This costs RAM, 8 times more, but for a PC based implementation RAM is usually plentiful and there is a speed and simplicity payoff for being able to address any cache bit with a single index number. All bytes in the cache are either 0x01 or 0x00 and each byte represents one cache bit.
The cache should be filled with a seed, this was accomplished by loading a file and repeating it throughout the cache until the cache is full (or using a file >= cache size to fill the cache). Generally a text file was used.
The C/C++ code below was just copied directly from my Windows software with no attempt to tidy it up. It is a bit clunky but is fully workable as a Black RNG Algortihm that you should be able to adapt to your own C software. No payment is required but please mention me as the author of the code and Black RNG algorithm.
//===========================================================================
// GENERATE_ENTROPY (Black RNG algorithm - see www.RomanBlack.com)
//===========================================================================
void __fastcall generate_entropy(void)
{
long i=0;
long e=0;
long pos=0;
long next_pos=0;
long engine_pos=0;
long engine_last_pos=0;
unsigned char mask=0;
unsigned char engine_value=0;
unsigned char engine_last_value=0;
long shuffle_count=0;
long loops=0;
long bar_count=0;
unsigned char c=0;
unsigned char bit=0;
unsigned char last_bit=0;
unsigned char astring[32]; // for reading Edit box!
signed long max_loops=0;
//--------------------------------------------------
// This generates 1Mb of entropy data from the
// 1Mbit seed data;
// starts with 1Mb seed already in seed_data[]
// copies into 8Mb in ent_data[] (this is the working "cache")
// performs the scrambling in ent_data[]
// ends with 8Mb in ent_data[] (1byte=1bit)
// Note! for indexing convenience the engine uses 1byte for each cache bit
//--------------------------------------------------
// clear progress bar
Form1->ProgressBar1->Position = 0;
//--------------------------------------------------
// first clean ent_data[]
for(i=0; i<8000000; i++) ent_data[i] = NULL;
//--------------------------------------------------
// copy 1Mb seed_data[] into 8Mb in ent_data[]
e=0;
for(i=0; i<1000000; i++)
{
// get the char
c = seed_data[i];
// if bit in c is set, then ent_data byte=1;
if( c & 0x80 ) ent_data[e+0] = 1;
if( c & 0x40 ) ent_data[e+1] = 1;
if( c & 0x20 ) ent_data[e+2] = 1;
if( c & 0x10 ) ent_data[e+3] = 1;
if( c & 0x08 ) ent_data[e+4] = 1;
if( c & 0x04 ) ent_data[e+5] = 1;
if( c & 0x02 ) ent_data[e+6] = 1;
if( c & 0x01 ) ent_data[e+7] = 1;
// move to next pos (next 8 bytes) in ent_data
e += 8;
}
//--------------------------------------------------
// next do the scrambling!!
//--------------------------------------------------
// Black RNG scramble procedure;
// 1. exchange the picked up bit at current pos
// 1b. shift that new bit into mask (ie keep record of last 8 bits)
// 2. toggle the following bit
// 3. using X value from engine, move forward X bits
// 4. inc engine one cylinder
// 5. check last 8 exchanged bytes, if == mask; (1 chance in 256)
// 5a. exchange engine value (shuffles engine)
// Repeat (until scrambled enough)
//--------------------------------------------------
#define ENG_SIZE 17 // number of cylinders
// load the engine with our 17 cylinder values (refine these later after testing?)
engine_last_value=9; // held value at the start, ready to exchange
engine[0] = 1; // these values work well enough
engine[1] = 2;
engine[2] = 3;
engine[3] = 1;
engine[4] = 2;
engine[5] = 3;
engine[6] = 4;
engine[7] = 5;
engine[8] = 7;
engine[9] = 1;
engine[10] = 2;
engine[11] = 3;
engine[12] = 6;
engine[13] = 4;
engine[14] = 1;
engine[15] = 3;
engine[16] = 11; // one larger prime value breaks up patterns
//--------------------------------------------------
// prepare to loop and scramble the data
loops = 0;
bit = 0;
last_bit = 0;
mask = 0;
shuffle_count = 0;
// allows user to change max number of loops on main form!
// must read the edit box and convert to a number...
long length = Form1->Edit1->GetTextLen(); // get length
Form1->Edit1->GetTextBuf(astring,(length+1)); // get text, add 1 for NULL
tstring[length] = NULL; // add the null
max_loops = atol(astring); // get as number
if(max_loops > 500)
{
max_loops = 500;
Form1->Edit1->Text = "500";
Form1->Edit1->Repaint();
}
if(max_loops < 1)
{
max_loops =1;
Form1->Edit1->Text = "1";
Form1->Edit1->Repaint();
}
// set up progress bar
Form1->ProgressBar1->Max = max_loops;
// loop and scramble the data
while(loops < max_loops)
{
// 1. exchange the picked up bit at current pos
bit = ent_data[pos]; // pick up new bit
ent_data[pos] = last_bit; // drop old bit
last_bit = bit; // save bit for next exchange
// 1b. shift that new bit into mask (ie keep last 8 bits)
mask = (mask << 1); // shift all bits left
mask = (mask & 0xFE); // safe! force clear bit0
if(bit != 0) mask += 0x01; // put in the new bit
// 2. toggle the following bit
next_pos = (pos + 1); // get pos of the next bit
if(next_pos == 8000000) next_pos=0; // handle cache wrap around
if(ent_data[next_pos] == 0) ent_data[next_pos]=1; // now toggle it
else ent_data[next_pos]=0;
// 3. using X value from engine cylinder, move forward X bits
pos += engine[engine_pos]; // move X bits forward
if(pos >= 8000000) // handle wrap
{
pos = (pos - 8000000); // loop pos
loops++; // count 1 more cache loop done!
// also handle progress bar updating here
// update progress bar every 5 loops
bar_count++;
if(bar_count >= 5)
{
Form1->ProgressBar1->Position = loops;
bar_count = 0;
}
}
// 4. inc engine one more cylinder, loop if needed
engine_pos++;
if(engine_pos >= ENG_SIZE) engine_pos=0;
// 5. check last 8 exchanged bytes; if == mask; (1 chance in 256) then;
// 5a. exchange engine value (shuffles engine)
if(mask == 0x2C) // b'0010 1100' randomish mask value
{
// shuffle (exchange) an engine cylinder value
engine_value = engine[engine_pos]; // save a copy of the current cylinder
engine[engine_pos] = engine_last_value; // held cyl -> current cyl
engine_last_value = engine_value; // current cyl -> held cyl
shuffle_count++; // count how many times engine cylinders have been shuffled
}
}
//--------------------------------------------------
// all done!
Form1->ProgressBar1->Position = Form1->ProgressBar1->Max;
sprintf(tstring,"Loops: %ld Engine shuffles: %ld",
loops,shuffle_count);
Form1->Label3->Caption = tstring; // display stats
}
//---------------------------------------------------------------------------
Fine-tuning the RNG
Here are some basic guidelines for setting up a Black RNG.
The cache size should be quite large. 1 Mbit or 8Mbit is good and at 8Mbit it produces >8000 engine shuffles per pass through the cache with an 8bit test mask.
If using a smaller cache, use a smaller test mask (ie 6bit or 5bit) to still give plenty of engine shuffles per pass through the cache. Also as discussed above if using a small cache there can possibly be a benefit to using a cache size that is a prime number.
Engine size (number of cylinders) should be a minimum of about 17+1 as used in my test RNG. If the cache must be small to preserve RAM on a smaller implementation, using more cylinders can help increase the max_states. It is possible that using a very large number of cylinders may compromise entropy by allowing the engine itself to patternise. I would keep the number of cylinders in the 15 to 25 range.
As for choosing cylinder values, about half the cylinder values should be small; 1,2,3. For the remainder use medium sizes 4-9 with the majority being odd if you have many cylinders, although I would include one of each value for maximum entropy. Then at least one larger value for every 10 cylinders or so.
Extracting random data from the RNG
All the information given above is for the base implementation of the Black RNG, and all it does is scramble it's own cache.
For applications where you only need a small amount of random data you could just extract a chunk of data from the cache. However this produces some issues. As the RNG is chaotic its main operation is to constantly smash any patterns that appear in its cache. For this reason, if you just extract the entire cache at any point in time this represents a worst case scenario where the cache contents are highly random but the cache is very unlikely to contain a mass of patterns at any one time. It is verging on being "too" random.
This represents a statistical bias, as real random data has a possibility of being a "mass of patterns" (although this is always a very small possibility).
It was always my intention that the output of this RNG is not its cache itself but is bits extracted over time. The RNG and the cache should be viewed as a "resource" that generates entropy so that data can be extracted over time.
The obvious and my "standard" method would be to extract every bit processed, specifically; to extract each transposed bit after each engine event. This works very well and produces a stream of bits with a volume of about 27% of cache size (with my cylinder values) so it generates around 2.1 million very good random bits per pass through a 8000000 bit cache.
As the RNG is good at producing an unknown value in any cache bit at any time, the data extracted in this way more closely resembles data extracted from other entropic sources like physical ones and as less data is extracted per pass through the cache (ie; extract 1 held bit per N engine cycles) this becomes more so.
See lower down the page for ideas on more complex implementations of the RNG.
Test results for the RNG
25th Nov 2010. I downloaded John Walker's ENT.EXE test program which does a battery of tests on data generated by random number generators.
For the random data I just used the value in the Black RNG "cache", this is a worst case scenario as normally you would generate data on the fly as the engine progresses, with the least data extracted over time the higher the entropy. But, even with the worst case scenario the randomness of the data generated by the Black RNG appears very good;

Entropy testing results from Black RNG - 25 Nov 2010 Black RNG engine stats; seed = just a text file cache = 8000000 bits cylinders = 17+1held; 1,2,3,1,2,3,4,5,7,1,2,3,6,4,1,3,11 + 9 method to extract random data; just test the cache contents after X loops Results generated by John Walker's test software ENT.exe 2008, see; http://www.fourmilab.ch/random/ Results of 6 tests of first 120000 bytes of cache contents using the same seed, after the RNG has done X loops through the cache; Loops Entropy; Compress CHI square CHI square Arithmetic Monte Serial through (8 perfect) able distrib. percent Mean Carlo Pi Correlation cache; percent (256 (>10 & <90 (127.5 (0 percent (0 perfect) (0 perfect) perfect?) perfect) perfect) perfect) 10 7.998496 0 249.85 57.93 127.5368 0.03 -0.001880 12 7.998601 0 232.34 84.25 127.3019 0.45 -0.002216 30 7.998421 0 262.36 36.23 127.2908 0.06 0.003228 100 7.998554 0 240.86 72.86 127.6494 0.43 -0.003508 200 7.998371 0 270.20 24.52 127.5329 0.25 0.000122 500 7.998429 0 261.70 37.32 127.2676 0.04 -0.000545 My explanation of the test values, much is copied from John Walker's page; Entropy; The information density of the contents of the file, expressed as a number of bits per character. A value of 8 means the randomness is so dense (so few patterns) the data cannot be compressed. Compressable percent; Same as above. Chi Square test; The chi-square test is the most commonly used test for the randomness of data, and is extremely sensitive to errors in pseudorandom sequence generators. If the percentage is greater than 99% or less than 1%, the sequence is almost certainly not random. If the percentage is between 99% and 95% or between 1% and 5%, the sequence is suspect. Percentages between 90% and 95% and 5% and 10% indicate the sequence is almost suspect. From my limited understanding of statistics math this value will change greatly according to the actual contents of the data being tested and there is no "perfect" value, but percentages between 10 and 90 are considered officially statistically "random". (see examples below!) The low-order 8 bits returned by the standard Unix rand() function, yields; Chi square distribution for 500000 samples is 0.01, and randomly would exceed this value more than 99.99 percent of the times. While an improved generator [Park & Miller] reports; Chi square distribution for 500000 samples is 212.53, and randomly would exceed this value 97.53 percent of the times. Chi-square result of a genuine random sequence created by timing radioactive decay events; Chi square distribution for 500000 samples is 249.51, and randomly would exceed this value 40.98 percent of the times. Black RNG (after as few as 10 loops, matches performance of a radioactive decay RNG!); Chi square distribution for 120000 samples is 249.85, and randomly would exceed this value 57.93 percent of the times. Arithmetic Mean; This is simply the result of summing the all the bytes in the file and dividing by the file length. If the data is close to random, this should be about 127.5. If the mean departs from this value, the numbers generated are consistently high or low. Monte Carlo Pi; Each successive sequence of six bytes is used as 24 bit X and Y co-ordinates within a square. If the distance of the randomly-generated point is less than the radius of a circle inscribed within the square, the six-byte sequence is considered a *hit*. The percentage of hits can be used to calculate the value of Pi. For very large streams (this approximation converges very slowly), the value will approach the correct value of Pi if the sequence is close to random. A 500000 byte file created by radioactive decay yielded: Monte Carlo value for Pi is 3.143580574 (error 0.06 percent). Serial Correlation Coefficient; This quantity measures the extent to which each byte in the file depends upon the previous byte. For random sequences, this value (which can be positive or negative) will, of course, be close to zero. A non-random byte stream such as a C program will yield a serial correlation coefficient on the order of 0.5. Wildly predictable data such as uncompressed bitmaps will exhibit serial correlation coefficients approaching 1.
New data from revised windows software
I revised my Windows software to produce histograms (spectral distribution of data) and scattergraphs (data plotted as XY points).
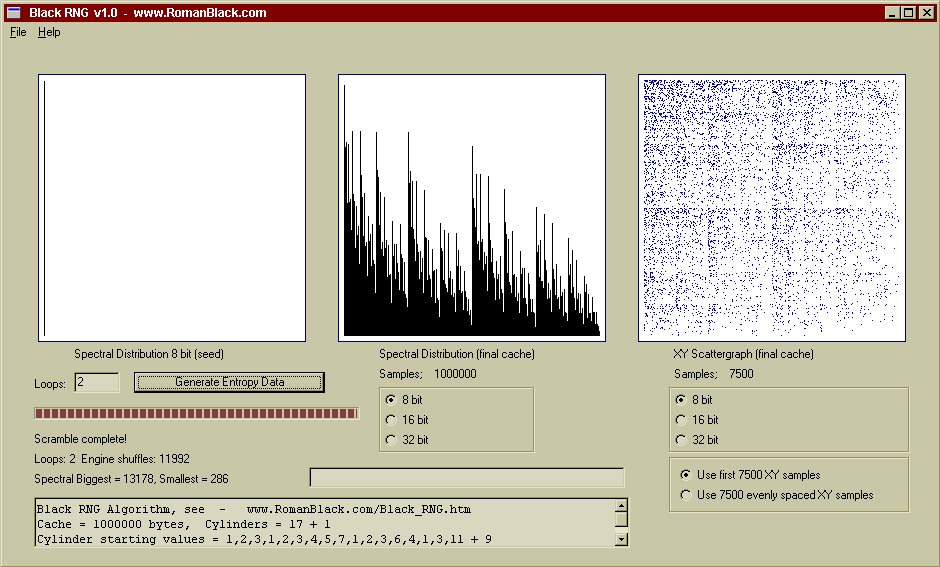
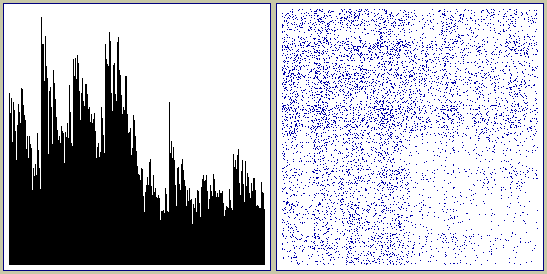
Above is a worst case, the seed is blank (all zeros) and after only 2 loops you can see it has stated to randomise the cache although it is nothing like good random data at this point.
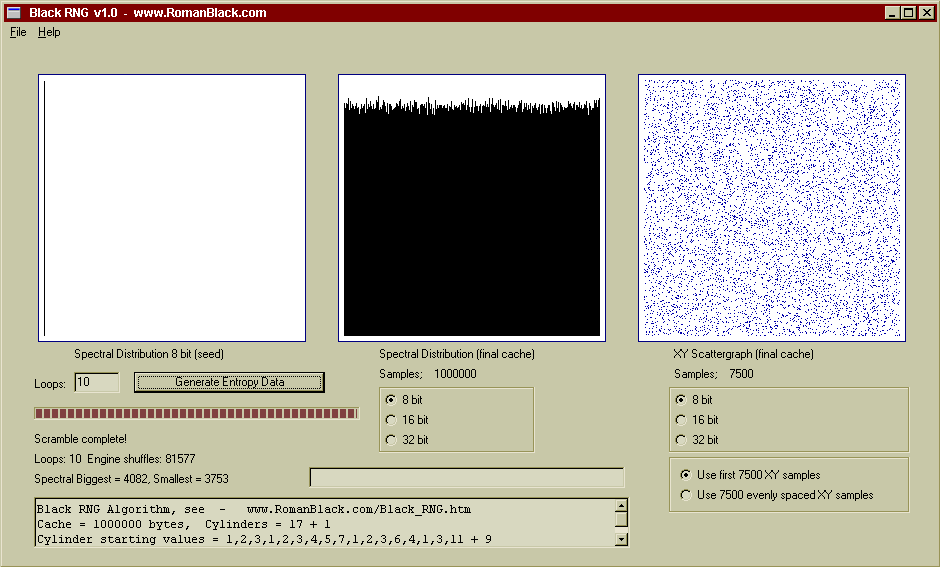
Above shows after 10 loops and >80000 engine shuffles it has randomised the cache even with the absence of a good seed.
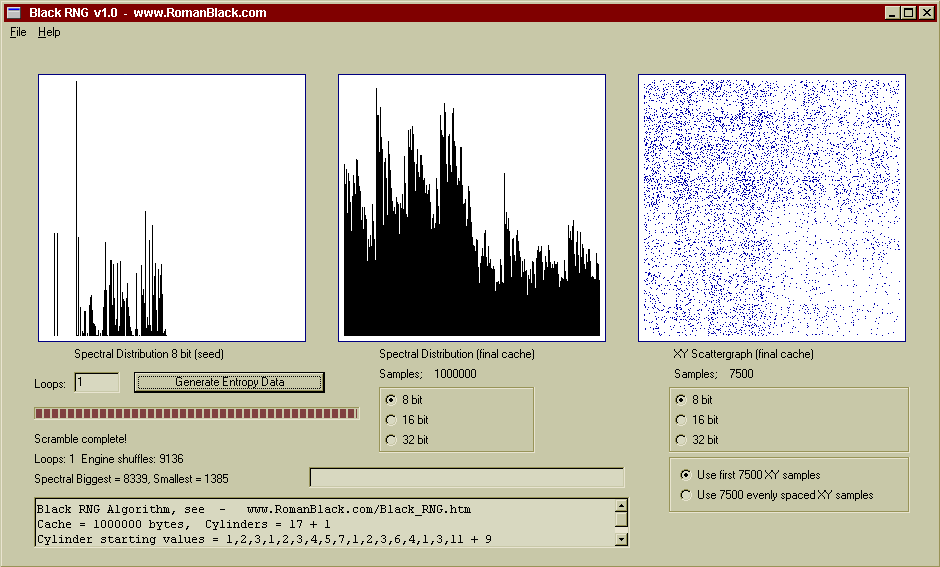
Above is a new seed, the same one I used for the "ENT.exe testing" further up the page, it is just a text file. After only one pass through the cache there is some significant randomisation happening.
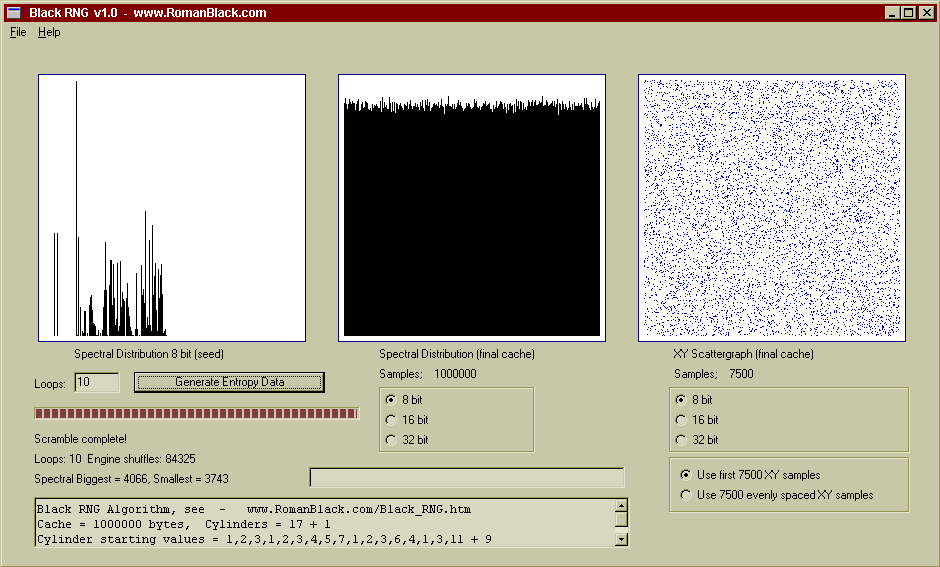
Above shows after 10 passes there is very high quality random data. The 1Mb file generated in the above 10 loop test is HERE if you want to do your own entropy testing on it.
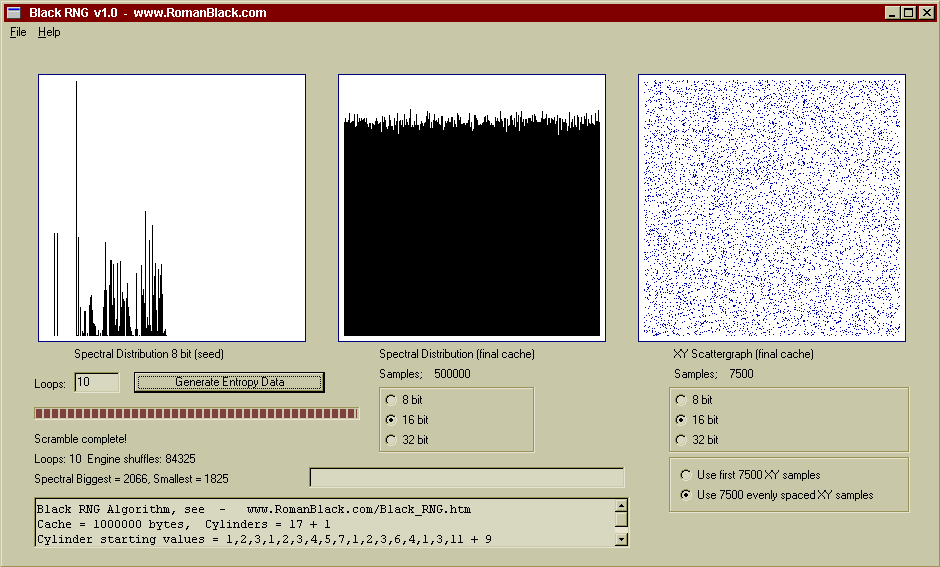
Above is the same cache contents, this time displayed as 16bit values. Good random data will look the same whether analysed as 8bit numbers or as 16bit or 32bit numbers. Also this scattergraph was plotted from samples spread throuhout the cache instead of just from the start of the cache. Again, with good random data this will make little difference.
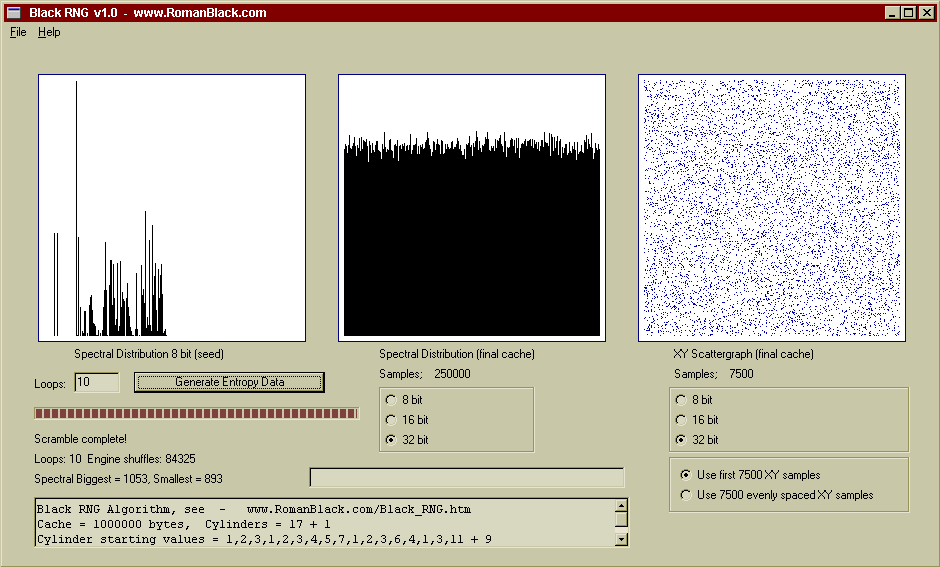
Above is the same cache contents, this time displayed as 32bit values. The spectral distribution is as good as with 8bit and 16bit numbers as shown by the histogram, however there are 4 times less samples to graph so the deviation is slightly higher (which is correct).
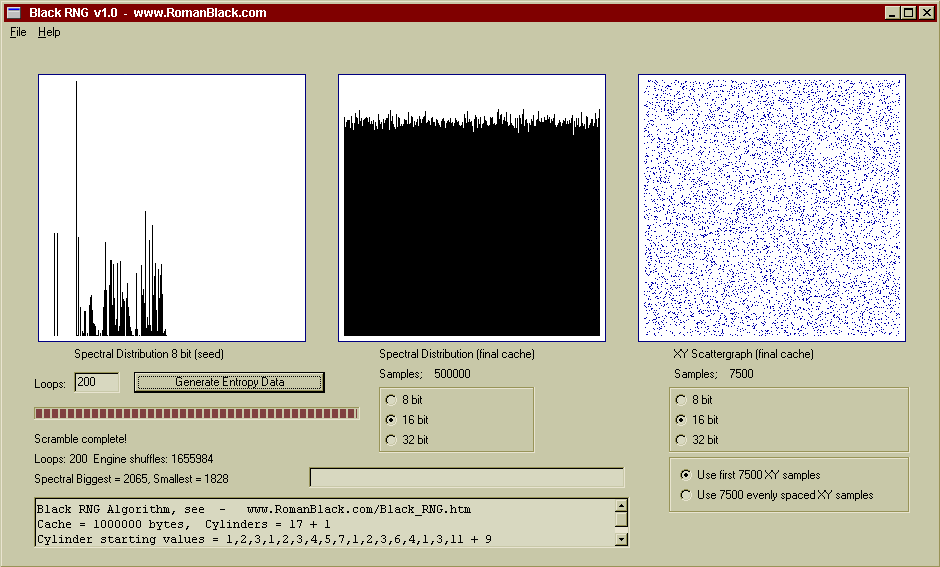
Above is a 200 loop test, generated from the same seed. After 200 loops the spectral distribution is still excellent as is the entropy, this is the same 200 loop test as shown above in the ENT.EXE testing.
Testing a smaller version of the RNG

Above is a 10 million loop test, performed as a "poor case scenario" in an attempt to get the engine to fail.
RNG setup;
Seed = all zeros!
Cache size = 6400 bits
Cylinders = 17+1 {1,2,3,1,2,3,4,5,7,1,2,3,6,4,1,3,11,9}
Mask = 8 bits
Even after 10 million loops the entropy in the cache was still of excellent quality. However this engine is not recommended, it is severely compromised due to these factors;
1. The cache was seeded with all zeros, a poor seed.
2. The cache is too small and is a multiple of 32 bits (data testing was also 32 bits).
3. Due to an 8bit mask there were only 6.6 engine shuffles per pass!

Above shows the results from a much improved RNG using a similar sized cache.
RNG setup;
Seed = a text file
Cache size = 6401 bits
Cylinders = 17+1 {1,2,3,1,2,3,4,5,7,1,2,3,6,4,1,3,11,9}
Mask = 5 bits
After 10 million loops the entropy in the cache was still of excellent quality. The difference in appearance of data from the 2 engines is due to different sample sizes being plotted. Both produced good cache entropy. However the second engine is superior due to using a cache that is not a multiple of 32 bits (a prime cache size would be even better still) and the important change to a 5 bit mask so that instead of 6.6 engine shuffles per loop the second engine produced 52.9 engine shuffles per loop. It also started with a better seed, although that is less critical.
It appears that smaller Black RNG engines can still produce good entropy although since the cost of a large cache is only RAM with no speed cost it is recommended that a large cache be used if possible.
NEW! 26th Nov 2010 - Black RNG Software
As seen in the above screenshots. So you can do your own tests or generate 1Mbyte of entropic data.
Black RNG v1.0 Software HERE